PEMBAHASAN
Data :
a.
Ringkasan numerik dari
data diatas:
Menggunakan Numerical
Summaries
Adapun penjelasan dari gambar data
diatas adalah:
|
1
|
Mean
(Rata Rata)
|
281.3721
|
|
2
|
Standart
Deferensiasi
|
28.32131
|
|
3
|
IQR
(Inter Quartil Range)
|
34.5
|
|
4
|
Data
Terendah
|
221
|
|
5
|
Quartil
1
|
264
|
|
6
|
Quartil
2 (Median)
|
289
|
|
7
|
Quartil
3
|
298.5
|
|
8
|
Data
tertinggi
|
338
|
|
9
|
n
(Jumlah Anggota)
|
43
|
Ket: Data
terendah, nilainya didapatkan dari persentase 0%.
Quartil 1, nilainya didapatkan dari
persentase 25%.
Quartil 2 (Mean), nilainya
didapatkan dari persentase 50%.
Quartil 3, nilainya didapatkan dari
persentase 75%.
Data tertinggi, nilainya didapatkan
dari persentase 100%.
Menggunakan
Active Data Set
Dari output di atas dapat diketahui
nilai ringkasan numeriknya, yaitu nilai harga statistik terendah adalah 221
(Min) sedangkan yang tertinggi adalah 338 (Max), rata-rata (Mean) nilainya
281.4 , nilai kuartil 1 (1st Qu), median, dan kuartil 3 (3rd Qu) berturut-turut
adalah 264, 289, dan 298.5.
b.
Diagram batang dan daun
dari data diatas adalah
Keterangan output:
a.
Leaf unit (unit daun/ satuan) sebesar 1 atau sepersatuan.
b.
Kolom tengah menunjukkan batang
dan kolom paling kanan menunjukkan daun.
c.
Jika
data terdiri atas angka-angka ratusan, maka bagian batang memuat angka ratusan
dan puluhan, sedangkan bagian daun memuat angka satuan. Contoh : Jika 221, maka
angka 22 sebagai batang dan 1 sebagai daun.
d.
Jika
data terdiri atas angka-angka 1 sampai 9, maka bagian batang memuat angka 0,
sedangkan bagian daun memuat angka tersebut. Contoh : Jika 3, maka angka 0 sebagai
batang, dan 3 sebagai daun.
e.
Kolom paling kiri menunjukkan
frekuensi kumulatif lebih dari sama dengan (terletak di bawah (4)) dan kurang
dari sama dengan (terletak di atas (4)), sedangkan (4) menunjukkan bahwa median
dari data terletak pada baris tersebut.
c.
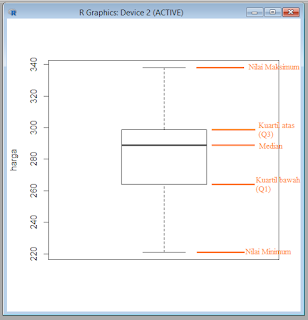
Diagram kotak dan titik
(boxplot) dari data diatas adalah
Terdapat
5 ukuran statistik yang bisa kita baca dari boxplot, yaitu :
·
Nilai minimum : nilai
observasi terkecil
·
Q1 : kuartil terendah
atau kuartil pertama
·
Q2 : median atau nilai
pertengahan
·
Q3 : kuartil tertinggi
atau kuartil ketiga
·
Nilai maksimum : nilai
observasi terbesar
·
Selain itu, boxplot
juga dapat menentukan ada tidaknya nilai outlier dan nilai ekstrim dari data
pengamatan.
Dari gambar diatas, sepintas kita bisa
menentukan beberapa ukuran statistik, meskipun tidak persis sekali. Nilai
statistik pada badan Boxplot : Nilai median ≈ 289, Nilai Q1≈
264, Nilai Q3 ≈ 298, nilai
maksimum ≈ 338, nilai
minimum ≈ 221. Sebaran
data tidak simetris, tapi menjulur ke bawah (Positively Skewness).
d. Dari
data diatas dapat disimpulkan bahwa data tersebut tidak simetris karena jarak
antar kuartil tidak sama dan jarak jangkauan antar kuartil berbeda. Oleh karena
itu dilakukan trnsformasi data dengan menggunakan “Tangga Transformasi Tukey ”.
pemilihan transformasi dilakukan berdasarkan tipe juraian, yaitu menjurai ke
bawah, serta kuat atau tidaknya juraian.
Berikut
hasilnya :
Hasil transformasi menggunakan antilogX :
Terlihat boxplot sudah cukup simetris
pada transformasi X16. Sehingga transformasi yang cocok adalah X16,
karena jika mnggunakan transformasi antilogX juraiannya terlalu kuat.
e.
Ubahlah data numerik
diatas menjadi data kategori dengan ketentuan sebagai berikut :
Berikut adalah distribusi frekuensi
(jelaskan arti dari output), diagram lingkaran, dan diagram batang dari data
setelah menjadi kategori :
-
Data setelah menjadi
kategori
-
Distribusi Frekuensi
Dari
output di atas diperoleh harga rata – rata servis komputer dan laptop
tahun 2015 dengan kategori D berjumlah 7 macam harga, kategori E berjumlah 11
macam harga, kategori F berjumlah 21 macam harga dan kategori G berjumlah 4
macam harga. Sedangkan persentase pada masing-masing kategori yaitu D = 16.28 %,
E = 25.58%, F = 48.84% dan G = 9.30%.
-
Diagram Lingkaran
-
Diagram Batang


















Tidak ada komentar:
Posting Komentar